
Keywords
Mathematics education, Preparation for Future Learning, Design-based research, Higher education
Introduction
In the transition from secondary school mathematics to mathematics at university, students struggle with the abstractness of mathematical theories and the formal nature of the mathematical language. These difficulties are most evident in mathematics courses with a strong focus on generalizations and formalisms, such as the first-year course in linear algebra. From secondary school, students are familiar with learning algorithmic solution strategies using clear-cut ‘recipes’ that prepared them well for the procedural part of a linear algebra course at university. On the other hand, understanding the underlying concepts of these computational tools poses a much greater and novel difficulty. Research has shown that after a course in linear algebra, students are generally able to successfully apply algorithms to known linear algebra problems and to perform the computations correctly [Dorier 2002].
To make sense of a concept an instructor is trying to convey in a lecture, students build on their prior knowledge. If relevant prior knowledge is not readily available to the students during instruction, this sense-making process is jeopardized. We know that preparing students to see the novel concept by activating relevant prior knowledge before formal instruction positively influences learning [preparation for future learning; Schwartz 2004]. Specifically, approaches that prepare students for learning from formal instruction using a well-designed problem-solving activity, such as productive failure, were shown to improve students’ conceptual understanding and transfer [Kapur 2012].
Building on the teaching designs preparation for future learning and productive failure, we developed preparatory exercises as additional learning materials for a first-year linear algebra course for mechanical engineering students. The structure of mathematics courses at ETH usually consists of a series of lectures followed by homework exercises which are discussed in exercise classes. In the year-long linear algebra course for mechanical engineers at ETH, we extended this cycle with preparatory homework exercises for five concepts per semester. The students hand these exercises in before attending the corresponding lecture. Figure 1 illustrates how the course structure of the linear algebra course was changed to include preparatory exercises. The core concepts covered by preparatory exercises are listed in Table 1.

Figure 1. Course structure of the linear algebra course with preparatory exercises.
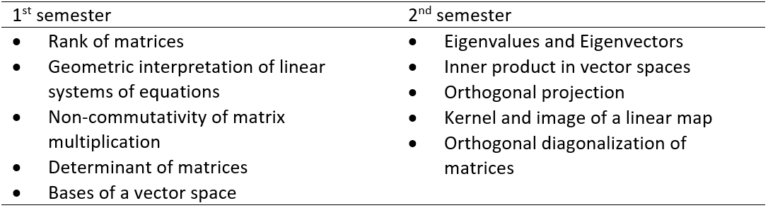
Table 1. List of concepts covered by preparatory exercises in the linear algebra course.
In the course of this project, we are investigating whether and how the addition of these preparatory learning opportunities to a first-year linear algebra course impacts students’ conceptual understanding. In a second step, we will analyze how these additional exercises influence student learning by identifying the underlying learning mechanisms. In the third part this project, we will investigate whether a deeper understanding of linear algebra concepts improves mechanical engineering students’ ability to tackle engineering problems in their further studies and future careers.
Research questions
Our work will contribute to the growing body of research on problem-solving before instruction (PS-I) designs in determining how PS-I can be integrated in a university mathematics course targeting highly abstract and formal concepts, and how such an implementation impacts students’ learning. Specifically, we want to answer the following research questions: Does the active participation in preparatory exercises improve mechanical engineering students’ conceptual understanding of linear algebra? What are the learning mechanisms involved? Does the active participation in preparatory exercises in linear algebra transfer to engineering domains?
These questions divide our project into three interdependent parts, visualized in Figure 2: Does it work? Why does it work? Does it transfer?

Figure 2. Main research questions of the linear algebra project
In the first part, we will investigate whether and how participation in the preparatory exercises influences students’ conceptual understanding of linear algebra. To this end, we evaluate students’ performance in the end-of-year exam and two additional tests on conceptual understanding that are administered to the students in the end of every semester. In an iterative design process, we revise the developed materials and measurement instruments for every iteration based on the data collected.
In the second part of the project, we will investigate in more detail how the preparatory exercises influence students’ learning by identifying the underlying mechanisms. This involves investigating whether proposed mechanisms from productive failure and preparation for learning research facilitate learning in our intervention, such as knowledge gap awareness, activation of prior knowledge, encoding of relevant features, and an increase in motivation.
Having identified the effect and its underlying mechanisms of the preparatory learning interventions on students’ conceptual understanding, we turn to the motivation of teaching linear algebra to engineering students in the third part of the project. Given that a linear algebra course in the first year of the curriculum in a mechanical engineering program should prepare students to tackle engineering problems in their further studies and future careers, we will investigate whether a deeper understanding of linear algebra concepts improves students’ ability to do so.
State of the project
The intervention started in Fall semester 2018 and will go on until the end of Spring semester 2022. Based on the data collected, we iteratively revised and adapted the learning materials and measurement instruments. The results of the first two iterations paint an encouraging picture that will be readied for publication soon. We are currently collecting data on the learning mechanisms involved by analyzing students’ solutions to the preparatory exercises and evaluating surveys. For the third part, we are in the midst of developing suitable transfer problems to test students’ transfer of conceptual understanding of linear algebra to engineering.
Publications
Baumgartner, V. (2020). Linear Algebra: Problem Solving as Preparation for Learning. Annual Conference of the Junior Researchers of the European Association for Research on Learning and Instruction (EARLI), Porto, Portugal (Conference cancelled)
References
[Dorier 2002] Dorier, J.-L., & Sierpinska, A. (2002). Research into the Teaching and Learning of Linear Algebra. In D. Holton,M. Artigue, U. Kirchgraber, J. Hillel, M. Niss, & A. Schoenfeld (Eds.), The Teaching and Learning of Mathematics at University Level (Vol. 7, pp. 255–273). Kluwer Academic Publishers. https://doi.org/10.1007/0-306-47231-7_24
[Kapur 2012] Kapur, M., & Bielaczyc, K. (2012). Designing for Productive Failure. Journal of the Learning Sciences, 21(1), 45–83. https://doi.org/10.1080/10508406.2011.591717
[Schwartz 2004] Schwartz, D. L., & Martin, T. (2004). Inventing to Prepare for Future Learning: The Hidden Efficiency of Encouraging Original Student Production in Statistics Instruction. Cognition and Instruction, 22(2), 129–184. https://doi.org/10.1207/s1532690xci2202_1
Project team

Vera Baumgartner

Simona Daguati

Dr. Meike Akveld
Alumni



